Միանդամի ներկայացումը մեկ այլ միանդամի քառակուսու տեսքով

Տեսություն

Միանդամների բազմապատկումը և աստիճան բարձրացնելը

Միանդամների արտադրյալը այնպիսի միանդամ է, որի արտադրիչները տվյալ միանդամների բոլոր արտադրիչներն են:

Ուշադրություն

Միանդամների բազմապատկման ժամանակ պետք է հիշել, որ գործակիցները բազմապատկվում են, իսկ միևնույն փոփոխականների աստիճանացույցները՝ գումարվում:

Միանդամները բազմապատկելու համար պետք է՝

• բազմապատկել միանդամների գործակիցները,
• գումարել միևնույն հիմքերով աստիճանների ցուցիչները:

Օրինակ

ա) Հաշվենք միանդամների հետևյալ արտադրյալը՝ 3a²b⋅2ab³

1.  Որպեսզի արտահայտությունն ակնառու լինի, փոխենք արտադրիչների տեղերը`

3a²b⋅2ab³=(3⋅2)⋅(a²⋅a)⋅(b¹⋅b³)

2. Բազմապատկենք միանդամների գործակիցները, և միևնույն հիմքով աստիճանների ցուցիչները գումարենք`

(3⋅2)⋅(a²⋅a)⋅(b¹⋅b³)=6⋅a³⋅b⁴:

բ) Հաշվենք միանդամների հետևյալ արտադրյալը՝ 0,35xy⁴⋅(−15y²z²)

1. Հարմարության համար փոխենք արտադրիչների տեղերը`

0,35xy⁴⋅(−15y²z²)=0,35⋅(−15)⋅(x)⋅(y⁴⋅y²)⋅(z²)

2. Միանդամի −15 գործակիցը գրենք տասնորդական կոտորակի տեսքով՝

−0,2⋅0,35⋅(−15)⋅(x)⋅(y⁴⋅y²)⋅(z²)=0,35⋅(−0,2)⋅(x)⋅(y⁴⋅y²)⋅(z²)

3. Բազմապատկենք միանդամների գործակիցները, և գումարենք միևնույն հիմքով աստիճանների ցուցիչները՝

0,35⋅(−0,2)⋅(x)⋅(y⁴⋅y²)⋅(z²)=0,35⋅(−0,2)⋅(x)⋅(y⁴⁺²)⋅(z²)=−0,07⋅x⋅y⁶⋅z²=−0,07xy⁶z²

Միանդամի աստիճան բարձրացումը

Ուշադրություն

Միանդամը աստիճան բարձրացնելիս պետք է՝

• միանդամի գործակիցը բարձրացնել այդ աստիճան,
• միանդամի փոփոխական արտադրիչների աստիճանացույցները բազմապատկել այն աստիճանի ցուցիչով, ինչ աստիճան որ բարձրացվում է միանդամը:

Օրինակ

Հաշվենք միանդամի խորանարդը՝ (−2xy²)³:

1. Առանձնացնենք միանդամի արտադրիչները: Հիշենք, որ եթե աստիճանի ցուցիչը նշված չէ, ապա այն հավասար է 1-ի՝

(−2xy²)³=(−2)³⋅(x¹)³⋅(y²)³:

2. Յուրաքանչյուր արտադրիչ առանձին-առանձին խորանարդ բարձրացնենք: Հիշենք, որ փոփոխականների աստիճանացույցները բազմապատկվում են այն ցուցիչով, ինչ աստիճան որ բարձրացվում է միանդամը՝  

(−2)³⋅(x¹)³⋅(y²)³=(−2)³⋅(x^1⋅3)⋅(y^2⋅3)=(−2)⋅(−2)⋅(−2)⋅(x^1⋅3)⋅(y^2⋅3):

3. Բացասական արտադրիչը 3−րդ աստիճան բարձրացնելով` որպես գործակից ստանում ենք բացասական թիվ՝

(−2)⋅(−2)⋅(−2)⋅(x^1⋅3)⋅(y^2⋅3)=−8⋅x³⋅y⁶=−8x³y⁶:

Տրված միանդամը և նրա առջև մինուս նշան դրված միանդամը կոչվում են հակադիր միանդամներ:

Օրինակ՝ 8x³y⁶ = −8x³y⁶

Առաջադրանք՝ կարդալ տեսությունը, վարժ. 41 ա, բ, գ, դ, 43, 46 ա, գ, ե, է

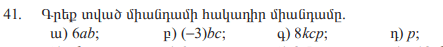
ա) 6ab=-6ab

բ) (-3)bc=3bc;

գ) 8kcp=-8kcp;

դ) p;=-p

ա) aba = a^2b^1                        ե) ababa = a^3a^2

բ) kpppkp = k^2p^4                  զ) 3a2a3a = a^8

գ) 3abab = 3a^2b^2                   է) a^3a^4 = a^7

դ) 7xxyyyyx = 7y^4x^3             ը) a^2a^3a^5 = a^10

Գտեք միանդամների արտադրյալին հավասար միանդամը (45-47)

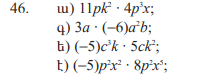
ա) 11п 2 · 4п 3 х=44п 4 л 2 х

բ) 15x 2 y 3· 8x 4 y=120x 6 y 4

գ) 3a·(-6)a 2 b= -18a 3 b

ե) (-5)c 3 k·5ck 2 =-25c 4 k 3

է) (-5)п 2 х 2 ·8 п 2 х 5 =40п 4 х 7