Рубрика: Երկրաչափություն

Թեմա՝ Պատկերացում գլանի մասին։

Ծանոթանանք տարածական այնպիսի մարմինների, որոնց մեջ շրջանագիծը նրա մասն է և ունի կարևոր դեր։ Սահմանում ` Ուղղանկյունը նրա որևէ կողմի շուրջը պտտումից առաջացած տարածական մարմինը կոչվում է գլան։ Գլանը ստանալու համար ուղղանկյունը պտտում ենք մի կողմի շուրջ։

Շրջանների կենտրոններով անցնող ուղիղը կոչվում է գլանի առանցք, շրջանները՝ գլանի հիմքեր, իսկ դրանց շառավիղները՝ գլանի շառավիղներ:Գլանի առանցքն ընդգրկող հարթությունը գլանի հետ ունի ընդհանուր մաս, որը կոչվում է գլանի առանցքային հատույթ:Գլանի առանցքային հատույթը ուղղանկյուն է, որի երկու հանդիպակաց կողմերը հիմքի տրամագծեր են: Իսկ մյուս երկու տրամագծեր չհանդիսացող կողմերը կոչվում են ծնորդներ:Գլանի ծնորդները հավասար են:

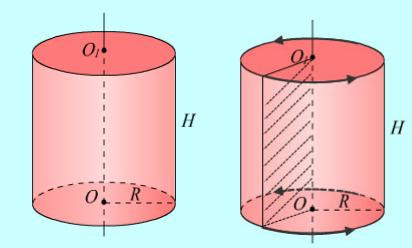
Գլանի կողմնային մակերևույթի բացվածքը ևս ուղղանկյուն է:

Հարցեր և առաջադրանքներ։

1․ Ո՞ր պատկերն է կոչվում գլան։ GEOGEBRA ծրագրով գծել գլան:

Ուղղանկյունը նրա որևէ կողմի շուրջը պտտումից առաջացած տարածական մարմինը կոչվում է գլան։

2․ Ինչպե՞ս կարելի է ստանալ գլան։

Գլանը ստանալու համար ուղղանկյունը պտտում ենք մի կողմի շուրջ։

3․ Ո՞րն է գլանի առանցքը, հիմքերը, շառավիղը, առանցքային հատույթը և ծնորդը։

Շրջանների կենտրոններով անցնող ուղիղը կոչվում է գլանի առանցք, շրջանները՝ գլանի հիմքեր, իսկ դրանց շառավիղները՝ գլանի շառավիղներ:

4․ Ի՞նչ պատկեր է գլանի առանցքային հատույթը։

Գլանի առանցքն ընդգրկող հարթությունը գլանի հետ ունի ընդհանուր մաս, որը կոչվում է գլանի առանցքային հատույթ:

5․Գլանի առանցքային հատույթը քառակուսի է: Գտեք գլանի ծնորդի և շառավիղի հարաբերությունը:

Եթե գլանի առանցքային հատույթը քառակուսի է, ապա գնալի ծնորդի և շառավիղի հարաբերությունը հավասար է 2:1:

6․ Գլանի առանցքային հատույթը 40սմ պարագծով մի ուղղանկյուն է, որի անկյունագծերը փոխուղղահայաց են: Գտեք գլանի շառավիղը:

40:4=10 (մի կողմ)

10:2=5 (շառավիղ)

7․Գլանի առանցքային հատույթը մի ուղղանկյուն է, որի անկյունագիծը ծնորդ հանդիսացող կողմի հետ կազմում է 60⁰-ի անկյուն: Գտեք այդ անկյունագիծը, եթե գլանի ծնորդի երկարությունը 6սմ է:

90-60=30
6×2=12 (անկյունագիծ):

8․ Գլանաձև բաժակը կիսով չափ լցված է թեյով: Գոլորիշիանալուց հետո թեյի հետքը մնացել էր բաժակի պատերին: Երկրաչափական ի՞նչ պատկեր է այդ հետքը:

Այդ պատկերն շրջանագիծն է:

9․ Գլանաձև ցիստեռնի մի մասը լցված է հեղուկով: Ի՞նչ պատկեր է հեղուկի մակերևույթը: Դիտարկեք ցիստեռնի տեղադրման երկու դեպք՝ ուղղաձիգ և հորիզոնական:

Ողղաձիգի դեպքում շրջանագիծ, հորիզոնականի դեպքում՝ ուղղանկյուն:

Թեմա՝ Շեղակյուն
Շեղանկյուն կոչվում է այն զուգահեռագիծը, որի բոլոր կողմերը հավասար են:

Շեղանկյան հատկությունները․

Քանի որ շեղանկյունը զուգահեռագիծ է, ապա այն ունի զուգահեռագծի բոլոր հատկությունները:

1. Շեղանկյան հանդիպակաց կողմերը հավասար են՝ AB=BC=CD=AD (քանի որ հավասար են բոլոր կողմերը):

2. Շեղանկյան հանդիպակաց անկյունները հավասար են՝ ∢A=∢C, ∢B=∢D:

3. Շեղանկյան անկյունագծերը հատման կետով կիսվում են՝ BO=OD, AO=OC

4. Շեղանկյան կողմին առընթեր անկյունների գումարը 180° է՝ ∢A+∢D=180°

Միայն շեղանկյանը բնորոշ հատկություններ.

5. Շեղանկյան անկյունագծերը փոխուղղահայաց են՝ AC⊥BD

6. Շեղանկյան անկյունագծերը նաև անկյունների կիսորդներ են (անկյունները կիսում են)

7. Անկյունագծերը շեղանկյունը բաժանում են չորս հավասար ուղղանկյուն եռանկյունների՝ ABO, CBO, CDO, ADO եռանկյունները հավասար ուղղանկյուն եռանկյուններ են:

Հարցեր և առաջադրանքներ
1.Ո՞ր պատկերն է կոչվում շեղանկյուն։

Շեղանկյուն կոչվում է այն զուգահեռագիծը, որի բոլոր կողմերը հավասար են:

2.GEOGEBRA ծրագրով գծեք ABCD շեղանկյուն, նշեք շեղանկյուն հավասար կողմերը։

AB=BC=CD=AD

3. GEOGEBRA ծրագրով գծեք ABCD շեղանկյուն, գծեք անկյունագծերը, ինչպիսի՞ անկյուն են կազմում շեղանկյան անկյունագծերը։

4. Գտեք շեղանկյուն բոլոր անկյունների աստիճանային գումարը։ Ո՞ր բանաձևով հաշվեցիր։

(4-2)x180=360^օ

5. Նշեք շեղանկյուն մի կողմին առընթեր անկյունների գումարի աստիճանային չափը։

180^օ

6. Նշեք շեղանկյանն բնորոշ որևէ հատկություն։

Անկյունագծերը շեղանկյունը բաժանում են չորս հավասար ուղղանկյուն եռանկյունների՝ ABO, CBO, CDO, ADO եռանկյունները հավասար ուղղանկյուն եռանկյուններ են:

7.Շեղանկյան մի կողմը հավասար է 12սմ 5մմ։ Գտեք շեղանկյան պարագիծը։

12+12+0,5+0,5=25սմ

8․Շեղանկյան անկյուններից մեկը 2 անգամ մեծ է մյուսից: Գտեք շեղանկյան բոլոր անկյունները:

x + 2x + x + 2x = 360^օ
6x = 360^օ
x = 60^օ
60×2=120^օ

9․ Գտեք շեղանկյան սուր անկյունը, եթե նրա երկու անկյունների տարբերությունը 18° է:
x + x + 18 +x + x + 18 = 360^օ
4x + 36 = 360^օ
4x = 324^օ

10. Շեղանկյան սուր անկյունը հավասար է 60°, իսկ պարագիծը 48մ է: Գտեք շեղանկյան փոքր անկյունագիծը:

11․ Գտիր ABCD շեղանկյան BD-ն և AO-ն, եթե OD=3 սմ, AC=14 սմ:
BD = 6սմ
AO = 7սմ

12․ Գտեք  շեղանկյան մյուս անկյունները, եթե A անկյունը 67° է:
67^օ, 67^օ, 113^օ, 113^օ

Խառը խնդիրներ ուղղանկյան, զուգահեռագծի, սեղանի վերաբերյալ

1. Ուղղանկյան կից կողմերը 12սմ և  25սմ են։ Գտեք ուղղանկյան պարագիծը։

12+12+25+25=74

2. AD և BC հիմքերով սեղանի մեջ AB=CD։ Ինչպիսի՞ սեղան է  ABCD-ն։

Հավասարասրուն։

3. O-ն   ABCD զուգահեռագծի անկյունագծերի հատման կետն է։ Ի՞նչ է   AO-ն  ABD եռանկյան համար։

Միջինագիծ

4. Հավասարասրուն սեղանի սրունքը հավասար է փոքր հիմքին և մեծ հիմքից փոքր է երկու անգամ։ Գտեք սեղանի պարագիծը, եթե փոքր հիմքը 7 է։

35սմ

5.Ուղղանկյան պարագիծը 20 սմ է: Որքա՞ն կարող է լինել այդ ուղղանկյան կողմի առավելագույն երկարությունը: Ուղղանկյան կողմերի երկարությունները արտահատվում են ամբողջ թվերով:

Առավելագույն կողմը կլինի 9սմ, 1

Նվազագույն կողմը կլինի 1սմ

6. Քանի՞ ուղիղ անկյուն ունի ուղղանկյուն սեղանը։

2

7. BC և   AD  հիմքերով ուղղանկյուն սեղանում  <B=90^0 է,  C կետից տարված է CK  բարձրությունը։ Ապացուցեք, որ AK=BC:

CK-ն գտնվում է սեղանից դուրս։ Մենք կարող ենք ասել, որ <BCK = 90^o, |=> ABCK-ն ուղղանկյուն է, |=> AK = BC:

8.Ուղղանկյան պարագիծը 60սմ է։ Գտեք ուղղանկյան կողմերը, եթե նրա կից կողմերը հարաբերում են ինչպես 1:9-ի։

9. ABCD ուղղանկյան անկյունագծերը հատվում են О կետում։ Գտեք АОB եռանկյան պարագիծը, եթե <CAD=30^0, АC=12 սմ։

AOB_{պարագիծ} = 18սմ

10. Գտեք ABCD ուղղանկյան պարագիծը, եթե  A  անկյան կիսորդը տրոհում է  BC կողմը   45, 6սմ և  7, 85սմ երկարությամբ հատվածների։

P_ABCD = 198.1սմ

11. ABCD զուգահեռագծի B  գագաթից АD կողմին տարված է  BH բարձրությունը, որ AB կողմի հետ կազմում է 40 աստիճանի անկյուն։ Գտեք զուգահեռագծի բոլոր անկյունները։

60^օ, 60^օ, 130^օ, 130^օ:

12. Զուգահեռագծի պարագիծը 100սմ է:Նրա կողմերից մեկը մյուսից մեծ է 10սմ-ով:Գտեք զուգահեռագծի կողմերը:

20սմ, 30սմ, 20սմ, 30սմ։

13. Զուգահեռագծի անկյուններից մեկը 50 աստիճանով մեծ է մյուսից:Գտեք զուգահեռագծի անկյունները:

65^օ, 115^օ, 65^օ, 115^օ։

14. O-ն   ABCD զուգահեռագծի անկյունագծերի հատման կետն է: Գտեք BO -ն և OC-ն, եթե  BD=12, AC=17։
OC = 8.5
BO = 6։

Ուղղանկյունը այն զուգահեռագիծն է, որի բոլոր անկյունները ուղիղ են։ Նկատենք, որ ուղղանկյունը կարող է դիտվել որպես զուգահեռագիծ, այսնինքն՝ այն օժտված է զուգահեռագծի բոլոր հատկություններով։
Ուղղանկյան անկյունագծերը հավասար են։

Ուղղանկյան հատկությունները․

Քանի որ ուղղանկյունը զուգահեռագիծ է, ապա այն ունի զուգահեռագծի բոլոր հատկությունները:

1. Ուղղանկյան հանդիպակաց կողմերը հավասար են՝ AB=CD, BC=AD

2. Ուղղանկյան յուրաքանչյուր անկյուն 90° է:

Հետևաբար, հանդիպակաց անկյունները հավասար են և կողմին առընթեր անկյունների գումարը 180° է:

3. Ուղղանկյան անկյունագծերը հատման կետով կիսվում են՝ BO=OD AO=OC

Նաև՝ BO=OD=AO=OC

4. Անկյունագիծը ուղղանկյունը բաժանում է երկու հավասար ուղղանկյուն եռանկյունների:

5. Անկյունագծին առընթեր խաչադիր անկյունները հավասար են:

6. Ուղղանկյան անկյունագծերը հավասար են՝ BD=AC

Ուղղանկյան չորս գագաթները լատիներեն մեծատառերով են նշանակում։  Կարելի է սկսել ցանկացած գագաթի տառից, բայց գագաթների հերթականությունը պետք է պահպանել:

Հարցեր և առաջադրանքներ։
1.Ո՞ր պատկերն է կոչվում ուղղանկյուն։

Ուղղանկյունը այն զուգահեռագիծն է, որի բոլոր անկյունները ուղիղ են։

2.GEOGEBRA ծրագրով գծեք ABCD ուղղանկյուն, նշեք ուղղանկյան  հավասար կողմերը։

AB = CD
AD = CB

3. GEOGEBRA ծրագրով գծեք ABCD ուղղանկյուն, գծեք անկյունագծերը, նշեք չորս կողմերը։

4. Գտեք  ուղղանկյան բոլոր անկյունների աստիճանային գումարը։ Ո՞ր բանաձևով հաշվեցիր։

(4-2)x180=360^o

5. Նշեք ոււղղանկյան մի կողմին առընթեր անկյունների գումարի աստիճանային չափը։

180^o

6. Նշեք ուղղանկյանը բնորոշ որևէ հատկություն։

Ուղղանկյան յուրաքանչյուր անկյուն 90° է:

Հետևաբար, հանդիպակաց անկյունները հավասար են և կողմին առընթեր անկյունների գումարը 180° է:

7. Ապացուցեք, որ այն զուգահեռագիծը, որի մի անկյուը ուղիղ է, ապա այն ուղղանկյուն է։

Եթե զուգահեռագծում մի անկյունը ուղիղ է ուրեմն նրա տակինն էլ լինելու ուղիղ քանի որ նրանք միակողմանի են։

Եթե զուգահեռագծում մի անկյունը ուղիղ է ուրեմն նրա հանդիպակաց անկյունն էլ կլինի ուղիղ։

8. Գտեք ABCD ուղղանկյան պարագիծը, եթե նրա կից կողմերը 12սմ, 50մմ են։

12+12+5+5=34

9. Ուղղանկյան լայնությունը 84սմ է, իսկ երկարությունը 6 սմ-ով մեծ է լայնությունից։ Գտեք ուղղանկյան պարագիծը։

ΑΒ=CD=84սմ

84+6=90

90×2+80×2=340

10. Հաշվիր ուղղանկյան պարագիծը, եթե հայտնի է, որ նրա լայնության և երկարության գումարը 46սմ  է։

11. Ուղղանկյան երկարությունը 26 սմ է, որը 6սմ -ով մեծ է լայնությունից։ Գտեք ուղղանկյան պարագիծը։

26-6=20

20×2+26×2=92

12. Ուղղանկյան անկյունագծերի հատման կետի հեռավորությունը մեծ կողմից 4սմ է, իսկ փոքր կողմից՝ 6սմ։ Գտեք ուղղանկյան պարագիծը։

40սմ

Խառը խնդիրներ ինքնուրույն աշխատելու համար

1. Տղան պնդում է, որ կարելի է գծել այպիսի բազմանկյուն, որի անկյունների գումարը 1800°է: Համաձա՞յն ես նրա հետ: Պատասխանդ հիմնավորիր։

Այո, քանի որ (12-2)x180=1800

2. Հաշվիր հնգանկյան բոլոր անկյունների աստիճանային գումարը:

(5-2)x180=540

3.Գտիր կանոնավոր վեցանկյան  անկյուններից յուրաքանչյուրի աստիճանային չափը:

(6 – 2)x180 = 720°
720:6 = 120°

4.Բերված պնդումներից ընտրիր ճիշտ պնդումները․
ա)Զուգահեռագծի անկյունագծերը զուգահեռ են:
բ)Զուգահեռագծի հանդիպակաց կողմերը զուգահեռ են:
գ)Զուգահեռագծի կից կողմերը զուգահեռ չեն:

5.Տղան չափեց զուգահեռագծի երկու անկյունները և ստացավ 27 և 164 աստիճանի մեծություններ: Արդյո՞ք նա ճիշտ էր չափել:

Ոչ

6. Զուգահեռագծի մի կողմը 22 սմ է, որը 6սմ-ով մեծ է մյուս կողմից։ Հաշվիր զուգահեռագծի պարագիծը:

22 + 22 + (22 + 6) + (22 + 6) = 100սմ

7. Տրված պնդումներից ընտրիր ճիշտ պնդումները զուգահեռագծերի վերաբերյալ:ա) Զուգահեռագծի անկյունների գումարը 540 աստիճան է:
բ) Զուգահեռագծի անկյունների գումարը 180 աստիճան է:
գ) Զուգահեռագծի անկյունների գումարը 360 աստիճան է:

8.Հաշվիր ABCD հավասարասրուն սեղանի անկյունները, եթե <A=30° է։

<A=<C=30^0

360-30+30=300

<B=300:2=150=<C

9.Սեղանի կողմերը հարաբերում են ինչպես՝ 7:6:10:9, իսկ սեղանի պարագիծը 128 սմ է: Հաշվիր սեղանի կողմերը:

7x + 6x + 10x + 9x = 32x

32x=128սմ

x=4

x/32 = 128սմ/32

a = 7x = 28սմ

b = 6x = 24սմ

c = 10x = 40սմ

d = 9x = 36սմ

a = 7x = 28սմ

b = 6x = 24սմ

c = 10x = 40սմ

d = 9x = 36սմ

10. Ուղղանկյուն սեղանի սուր անկյունը 45° է: Փոքր սրունքը 10 սմ է, իսկ մեծ հիմքը՝ 19 սմ: Գտիր սեղանի փոքր հիմքը և միջին գիծը։

Փոքր հիմքը՝ 19-10=9

Միջին գիծը՝ 19+9:2=14

Սեղանի միջին գիծ։
Սահմանում։ Սեղանի սրունքների միջնակետերը միացնող հատվածը կոչվում է սեղանի միջին գիծ:

Թեորեմ: Սեղանի միջին գիծը զուգահեռ է հիմքերին և հավասար է նրանց կիսագումարին:
Ապացույցը ինքնուրույն։

Առաջադրանքներ։

1.GEOGEBRA ծրագրով գծիր հավասարասրուն սեղան,  գծիր միջին գիծը։ Հավասարասրուն սեղանը քանի՞ միջին գիծ ունի։

1

2.GEOGEBRA ծրագրով գծիր ուղղանկյուն  սեղան,  գծիր միջին գիծը։ Ուղղանկյուն  սեղանը  քանի՞ միջին գիծ ունի։

1

3. Սեղանի հիմքերն  են 30սմ և 20սմ։ Գտեք սեղանի միջին գծի երկարությունը։

(30:2)+(20:2)=25

4. Սեղանի հիմքերը հարաբերում են, ինչպես 2 : 4, իսկ միջին գիծը 15 սմ է: Գտեք սեղանի հիմքերը:

(2x + 4x) / 2 = 15

(2x + 4x) = 15 * 2

6x = 30

x/6 = 30/6

x = 5սմ

a = 2x

b = 4x

a = 10սմ

b = 20սմ

5.Ուղղանկյուն սեղանի սուր անկյունը 45 աստիճան  է ։ Գտեք մնացած անկյունները։

360-90-90-45=135

6. Գտեք հավասարասրուն սեղանի անկյունները, եթե հայտնի է, որ սեղանի երկու անկյունների տարբերությունը 40 աստիճան  է:

110°, 110°, 70°, 70°:

7. Հավասարասրուն սեղանի մեծ հիմքը 4մ է, սրունքը՝ 2 մ, իսկ դրանց կազմած անկյունը՝ 60 աստիճան: Գտեք սեղանի փոքր հիմքը:

Քանի որ այս քառանկյունը հավասարասրուն է երկրորդ սրունքը նույնպես 2մ է։ Դա նշանակում է, որ երկրորդ անկյունը նույնպես 60°: 

8. M և N կետերը գտնվում են տրված ուղղի մի կողմում, և նրանց հեռավորությունները այդ ուղղից հավասար են 10 սմ և 22 սմ: Գտեք MN հատվածի միջնակետի հեռավորությունը այդ ուղղից:

16սմ

Թեմա՝ Սեղան

Սահմանում։ Սեղան է կոչվում այն ուռուցիկ քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը զուգահեռ չեն: Տես նկարը՝

Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր:
Նկարում AD -ն և BC -ն սեղանի հիմքերն են:  

Սեղանի կողմերը, որոնք զուգահեռ չեն, կոչվում են  սրունքներ:
AB -ն և CD-ն սեղանի սրունքներն են:  

Հիշիր։
Սեղանի  անկյունների գումարը (ցանկացած քառանկյան) 360° է:
Ցանկացած սեղանի սրունքին առընթեր անկյունների գումարը 180° է:

Սահմանում։
Սեղանը կոչվում է ուղղանկյուն սեղան, եթե նրա սրունքներից որևէ մեկը ուղղահայաց է հիմքերին, տես նկարը։

Նկարում AB -ն ուղղահայց է սեղանի հիմքերին։ <А, <B 90 աստիճան են։  

Սահմանում։
Սեղանը, որի սրունքները հավասար են, կոչվում է հավասարասրուն սեղան, տես նկարը։

Նկարում AB -ն և CD -ն սեղանի սրունքներն են և իրար հավասար են։
   Հարցեր և առաջադրանքներ․
1. Ո՞ր պատկերն է կոչվում սեղան, գրիր սահմանումը։
Սեղան է կոչվում այն ուռուցիկ քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը զուգահեռ չեն:

2. GEOGEBRA ծրագրով գծիր սեղան, նշիր սրունքները, հիմքերը, ո՞ր կողմերն են զուգահեռ։

Սրունքներ՝ AB, CD

Հատվածներ՝ BC, AD

Զուգահեռ են՝ ABIICD

3. Ո՞ր պատկերն է կոչվում  ուղղանկյուն սեղան, գրիր սահմանումը։

Սեղանը կոչվում է ուղղանկյուն սեղան, եթե նրա սրունքներից որևէ մեկը ուղղահայաց է հիմքերին։

4. GEOGEBRA ծրագրով գծիր ուղղանկյուն սեղան, նշիր սրունքները, հիմքերը, ո՞ր սրունքն է ուղղահայաց հիմքերին,  ո՞ր անկյուններն են 90 աստիճան։

Հիմքերը՝ BC, AD

Սրունեքները՝ AB, CD

<A=90^o, <B=90^o

Ուղղահայաց են՝ AB

5. Ո՞ր պատկերն է կոչվում հավասարասրուն սեղան, գրիր սահմանումը։

Սեղանը, որի սրունքները հավասար են, կոչվում է հավասարասրուն սեղան:

6. GEOGEBRA ծրագրով գծիր հավասարասրուն սեղան, նշիր սրունքները, հիմքերը, ո՞ր կողմերն են իրար հավասար։

Հիմքերը՝ BC, AD

Սրունեքները՝ AB, CD

AB=CD

7. GEOGEBRA ծրագրով գծիր սեղան, ո՞ր անկյունների գումարն է 180 աստիճան։

8. Ի՞նչի է հավասար սեղանի բոլոր  անկյունների  աստիճանային գումարը։

(n-2)x180=360

(4-2)x180=360

9. Նշիր ճիշտ պնդումը․
ա)Հավասարասրուն սեղանի սրունքները զուգահեռ են:
բ)Ուղղանկյուն սեղանի հիմքերը միշտ հավասար են:
գ)Ցանկացած սեղանի հիմքերը զուգահեռ են:

10. Նշիր ճիշտ պնդումը․ Սեղան կոչվում է այն քառանկյունը, որի
ա)կողմերը զույգ առ զույգ զուգահեռ են:
բ)երկու կողմերը զուգահեռ են, իսկ մյուս երկուսը՝ ոչ:

11. Նշիր ճիշտ պնդումը․ Սեղանը կոչվում է հավասարասրուն, եթե
ա)նրա սրունքները հավասար են:
բ)նրա սրունքները զուգահեռ են:

12. Տրված է ABCD սեղան, որտեղ  <A=37°, <C=121°: Գտիր՝ <B,<D-ն։
59^о, 143^о

13.Գտեք AD և BC հիմքերով սեղանի B և D անկյունները, եթե ∠A = 29°, ∠C = 117° է :
151^о, 63^о

14. Սեղանի հիմքերի հարաբերությունը հավասար է 2:7: Հաշվիր սեղանի մեծ հիմքը, եթե նրա փոքր հիմքը հավասար է 12 սմ:
42սմ

Թեմա՝ Զուգահեռագիծ

1. GEOGEBRA  ծրագրով գծեք ABCD զուգահեռագիծ, նշեք АB կողմին կից և հանդիպակաց կողմերը։

Կից՝ BC, AD

2. GEOGEBRA  ծրագրով գծեք ABCD զուգահեռագիծ, նշեք  А անկյան կից և հանդիպակաց անկյունները։

<A-կից՝ <Β, <D հանդ․ <C

3. Զուգահեռագծի բոլոր անկյունների աստիճանային գումարը ի՞նչ բանաձևով ես հաշվում։

(n-2)x180

n=4

(4-2)x180=360

4. Քառանկյան բոլոր կողմերը 5սմ են։ Կարո՞ղ ենք պնդել, որ այն զուգահեռագիծ է։

Այո, համաձայն II հայտանիշի։

5. GEOGEBRA  ծրագրով գծեք ABCD  քառանկյուն, այնպես որ անկյունագծերը հատման կետով կիսվեն։ Կարո՞ղ ենք պնդել, որ այդ քառանկյունը զուգահեռագիծ է։

Այո, համաձայն III հայտանիշի

6. Զուգահեռագծի անկյունագիծը երկու կից կողմերի հետ կազմում է համապատասխանաբար 25 աստիճանի և 35 աստիճանի անկյուններ: Գտեք զուգահեռագծի բոլոր անկյունները:

60°, 120°, 60°, 120°

7. Գտեք ABCD զուգահեռագծի անկյունները, եթե  ∠A = 80 աստիճան է։

80, 80, 180:

8. Գտեք ABCD զուգահեռագծի անկյունները, եթե  ∠A – ∠B = 55 աստիճան է։

180-55=125

125:2=62.5

62.5+55=117.5

9.  Գտեք ABCD զուգահեռագծի անկյունները, եթե ∠A + ∠C = 142 աստիճան է։
<A =71 ^o
<B =109 ^o
<C =71 ^o
<D = 109^o

10. Գտեք ABCD զուգահեռագծի անկյունները ,  եթե  ∠A = 2 * ∠B:
<A =120 ^o
<B =60 ^o
<C =120 ^o
<D = 60^o

11. Գտեք ABCD զուգահեռագծի անկյունները, եթե  ∠CAD = 16 աստիճան է, իսկ  ∠ACD = 37 աստիճան է։
<A =53 ^o
<B =127 ^o
<C =53^o
<D =127 ^o

12. Զուգահեռագծի պարագիծը  70 սմ է: Գտեք զուգահեռագծի կողմերը, եթե կողմերից մեկը վեց  անգամ մեծ է մյուսից:

5սմ, 30սմ

Թեմա՝ Զուգահեռագիծ

1. Զուգահեռագծի անկյուններկց մեկը  55° է: Գտիր զուգահեռագծի մյուս անկյունները:

55, 55, 125, 125

2. Զուգահեռագծի մի կողմը 29 սմ է, իսկ մյուս կողմը 7 սմ-ով մեծ է նրանից: Գտիր զուգահեռագծի պարագիծը:

29+7=36

29×2=58

36×2=72

72+58=130

3. Զուգահեռագծի կողմերը 10 և 15 են։ Գտիր Զուգահեռագծի պարագիծը:

10×2=20

15×2=30

30+20=50

4. Զուգահեռագծի անկյուններից մեկը մյուսից մեծ է 30 աստիճանով։ Գտիր զուգահեռագծի բոլոր անկյունները։

180-30=150

150:2=75

75+30=105

5. ABCD զուգահեռագծի մեջ օ-ն զուգահեռագծի անկյունագծերի հատման կետն է։ AOD եռանկյան պարագիծը հավասար է 25սմ, AC=16սմ, BD=14 սմ։ Գտի՛ր  BC-ն։

10

6. ABCD քառանկյունը զուգահեռագիծ է։ Ապացուցեք, որ եռանկյուն ABC հավասար է եռանկյուն ACD-ին։

Եռանկյունների հավասարության երրորդ հայտանիշ։
AB = DC
BC = AD
AC = AC

7. ABCD զուգահեռագծի А անկյունը  2  անգամ փոքր է B անկյունից։ Գտեք զուգահեռագծի բոլոր անկյունները։

60, 60, 120, 120

8.ABCD զուգահեռագծի մեջ օ-ն զուգահեռագծի անկյունագծերի հատման կետն է։  Գտեք BO և ОC-ն, եթե BD=12, AC=17:

BO = 6
OC = 8.5

9. ABCD զուգահեռագծի  A անկյան  կիսորդը  BC հատվածում հատում է k կետում  և տրոհում է  15 սմ  և 9սմ  հատվածների ։Գտի՛ր զուգահեռագծի պարագիծը ։

10. Գտեք զուգահեռագծի անկյունները, եթե դրանցից երկուսի գումարը 100 աստիճան է:

50, 50, 130, 130

Թեմա՝ Զուգահեռագծի հայտանիշները
Եթե տրված է քառանկյուն, ինչպես պարզել, այդ քառանկյունը զուգահեռագիծ է, թե՞ ոչ։ Տեսանյութը տես այստեղ։
Հայտանիշներ։

1. Եթե քառանկյան երկու կողմերը հավասար են և զուգահեռ, ապա քառանկյունը զուգահեռագիծ է:

2. Եթե քառանկյան հանդիպակաց կողմերը զույգ առ զույգ հավասար են, ապա քառանկյունը զուգահեռագիծ է:

3. Եթե քառանկյան անկյունագծերը հատվում և հատման կետով կիսվում են, ապա քառանկյունը զուգահեռագիծ է:

1.Կարելի՞ է պնդել, որ 4մ, 4մ, 6մ, 6մ կողմերով քառանկյունը զուգահեռագիծ է:
Ոչ

2.ABCD քառանկյան մեջ АB=CD։ Կարելի՞ է պնդել, որ քառանկյունը զուգահեռագիծ է
Ոչ

3.ABCD քառանկյան մեջ АB=CD, BC=AD: Կարելի՞ է պնդել, որ քառանկյունը զուգահեռագիծ է։
Այո

4.Ձևակերպիր զուգահեռագծի երեք հայտանիշները:
Եթե քառանկյան երկու կողմերը հավասար են և զուգահեռ, ապա քառանկյունը զուգահեռագիծ է:

Եթե քառանկյան հանդիպակաց կողմերը զույգ առ զույգ հավասար են, ապա քառանկյունը զուգահեռագիծ է:

Եթե քառանկյան անկյունագծերը հատվում և հատման կետով կիսվում են, ապա քառանկյունը զուգահեռագիծ է

5.Ուռուցիկ քառանկյան երկու անկյունների աստիճանային գումարը 180 է, գտեք մյուս երկու անկյունների աստիճանային գումարը։
180

6.ABCD ուռուցիկ քառանկյան մեջ AB=CD, <А=70աստիճան է, <D=110 աստիճան։ Ապացուցեք, որ քառանկյունը զուգահեռագիծ է։
Քառանկյան անկյունների աստիճանային չափերի գումարը 360օ է։ 360օ – 70օ – 110օ = 180օ: Մենք ուզում ենք ստանալ զուգահեռագիծ, ուրեմն մեզ պետք են ևս մեկ 70օ և 110օ անկյուններ՝ <B = 110օ, <C = 70օ:

7.ABCD քառանկյունը զուգահեռագիծ է։ Ապացուցեք, որ <BCA=<CAD։
Եթե

8.ABCD քառանկյան մեջ AB = CD և AB || CD, ∠C = 15 աստիճան : Գտեք քառանկյան բոլոր անկյունները։
15օ, 15օ, 165օ, 165օ

9.ABCD ուռուցիկ քառանկյան մեջ AB = CD, ∠B = 70 աստիճան , ∠BCA = 60 աստիճան , ∠ACD = 50 աստիճան: Ապացուցեք, որ քառանկյունը զուգահեռագիծ է։
AD = DC
Եթե <B = 70o, և <BCA = 60o, ուրեմն <BAC = 50o(180o – 70o – 60o)

AB = DC,
AC = AC,
<BAC = <ACD,
Եռանկյունների հավասարության 1–ին հայտանիշ
△ADC = △BAC:

10.Գտեք զուգահեռագծի անկյունները, եթե դրանցից երկուսի գումարը 80 աստիճան է:
40o, 40o, 140o, 140o

11.Գտեք ABCD զուգահեռագծի անկյունները, եթե՝
ա) ∠A = 84 աստիճան է ,
<B = 96o, <D = 96o, <C =84o
բ) ∠A – ∠B = 55 աստիճան է ,
<A = 117.5o , <B = 62.5o, <C = 117.5o, <D = 62.5o
գ)∠A + ∠C = 142 աստիճան է։
<A = 71o, <B = 109o, <C = 71o, <D = 109o

12.Դժվար։ Ապացուցուցե զուգահեռագծի առաջին հայտանիշը։
AB||CD, AB = CD,
|=> △ABC =△ACD(Եռանկյունների հավասարության 1-ին հայտանիշ),
|=> BC || AD(Վերևի տողում գրված անկյունները օգտագործում ենք որպես խաչադիր)