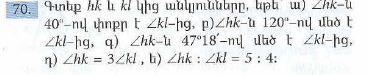Երկրաչափության ներածություն
Նոր առարկայի անվանումը ԵՐԿՐԱՉԱՓՈՒԹՅՈՒՆ է, այն առաջացել է հին հունարեն ԵՐԿԻՐ և ՉԱՓՈՒՄ բառերից:
Երկրաչափությունը հնագույն գիտություններից է և առաջացել է չափումների, սահմանների ընդլայնման, ճանապարհների և շենքերի կառուցման գործնական անհրաժեշտության կապակցությամբ: Հիմա մենք այն ճանաչում ենք որպես երկրաչափական պատկերների հատկություններն ուսումնասիրող գիտություն:
Հետագայում կտրվեն տարբեր պատկերների սահմանումներ, բացի երկուսից՝ կետ և ուղիղ: Այդ երկու պատկերների միջոցով մենք կսահմանենք մնացած բոլոր երկրաչափական պատկերները, իսկ կետն ու ուղիղը կարող ենք միայն փորձել պատկերացնել՝ կետը որպես անվերջ փոքր մի բան, իսկ ուղիղը՝ որպես մի բան, որն անվերջ տարածվում է երկու կողմի վրա:
Կետերը նշանակում են լատիներեն մեծատառերով, իսկ ուղիղները՝ փոքրատառերով: Կետի և ուղղի փոխադարձ դասավորվածությունը բառերով կարելի է նկարագրել տարբեր ձևերով.
1. կետը գտնվում է (ընկած է) ուղղի վրա կամ ուղիղն անցնում է (տարված է) կետով,
2. կետը չի գտնվում (ընկած չէ) ուղղի վրա կամ ուղիղը չի անցնում (տարված չէ) կետով:
Երկրաչափության մեջ այդ փաստերը գրում են նշանների միջոցով՝
1. A և B կետերը գտնվում են (ընկած են) a ուղղի վրա կամ a ուղիղն անցնում է (տարված է) A և B կետերով՝ A∈aևB∈a
2. C և D կետերը չեն գտնվում (ընկած չեն) a ուղղի վրա կամ a ուղիղը չի անցնում (տարված չէ) C և D կետերով՝ C∉aևD∉a
Երկրաչափության ամենակարևոր ենթադրություններից է հետևյալը` ցանկացած երկու կետերով կարելի է տանել ուղիղ, ընդ որում, միայն մեկը:
Հետևաբար, երբեմն ուղիղը կարող ենք նշանակել լատիներեն երկու մեծատառերով, օրինակ՝ AB ուղիղ, քանի որ այդ երկու կետերով ոչ մի ուրիշ ուղիղ հնարավոր չէ տանել:
Հետևաբար, երկու ուղիղներ կարող են ունենալ միայն մեկ ընդհանուր կետ և հատվել կամ չունենալ ոչ մի ընդհանուր կետ և երբեք չհատվել:
Նշանի միջոցով գրում ենք այսպես՝ a∩b=A
Ընդհանուր կետ չունեցող (չհատվող) ուղիղները կոչվում են զուգահեռ:
Նշանի միջոցով գրում ենք այսպես՝ a∥b
Ուղղի մի մասը, որը սահմանափակված է երկու կետերով, կոչվում է հատված:
Հատվածը նշանակում են այսպես՝ AB
Ուշադիր նայիր ներքևի նկարին:
Ուշադրություն
AB և CD հատվածները հատվում են, CD և DE հատվածներն ունեն ընդհանուր ծայրակետ, AB և HF, AB և DE, CD և HF, HF և DE հատվածները չեն հատվում:
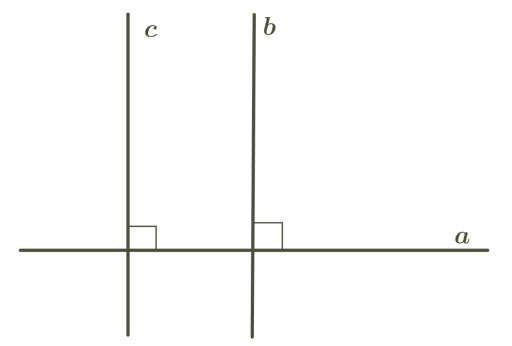
Բոլոր a, b և c ուղիղները հատվում են:
Քանի որ ուղիղը մեր պատկերացմամբ անվերջ տարածվում է երկու կողմի վրա, ապա վաղ, թե ուշ այդ ուղիղները կհատվեն, չնայած, որ նկարի վրա դա չի երևում:
Մենք կարողանում ենք նկարել անվերջ ուղղի միայն մի մասը:
Առաջադրանք դասարանում ՝
- Գտիր, թե ո՞ր պնդումներն են համապատասխանում C∉p գրառմանը.
- C ուղիղն անցնում է p կետով
- p ուղիղը չի անցնում C կետով
- C կետը p ուղղի կետ է
- C կետը չի գտնվում pուղղի վրա
- C կետը գտնվում է p ուղղի վրա
- p ուղիղը անցնում է C կետով
2.Նշիր ներքևի նկարին համապատասխանող պնդում(ներ)ը:
Պատկերված ուղիղները`
- չեն հատվում:
- զուգահեռ են:
- հատվում են:
3.Եթե հարթության վրա երկու ուղիղ զուգահեռ են, ապա դրանք չեն հատվում:
Ընտրիր՝ պնդումը ճի՞շտ է, թե՞ ոչ:
4.
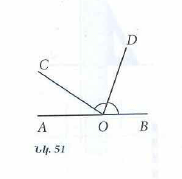
Ո՞ր պնդումներն են համապատասխանում տրված նկարին.
- O∉c ուղղին
- O∈c ուղղին
- O∈AB հատվածին
- O∉ABհատվածին
5.Գտիր ճիշտ պնդումները նույն հարթության վրա գտնվող կետերի և ուղիղների վերաբերյալ.
- Ոչ մի ուղղի վրա չկա երեքից ավելի կետ:
- Ցանկացած ուղղի վրա կան անվերջ թվով կետեր:
- Ցանկացած երկու կետերով անցնում է միակ ուղիղը:
- Ցանկացած երեք կետերով կարելի է տանել ուղիղ:
- Մեկ կետով կարելի է տանել միակ ուղիղը:
- Ցանկացած կետով անցնում են անվերջ թվով ուղիղներ:
- Որոշ երեք կետերով կարելի է տանել ուղիղ:
- Կա այնպիսի կետ, որով ոչ մի ուղիղ չի անցնում:
Առաջադրանք տանը՝
- վերջացնել դասարանային առաջադրանքը,
- վարժություն-1, 4, 6,7
- լրացուցիչ վարժություն – 2, 5